Html – Get the largest rectangle possible when the corners of the rectangle are cut

So we have a rectangle with, let’s say dimensions of 120ft length, 72ft breadth and 20mm thickness (we assume thickness is negligible thus consider this cuboid a 2D rectangle). I want to use JavaScript to make a function, such that if any rectangular regions are cut from the corners of this rectangle, I can still find the largest chunk possible.

Here’s my approach but it’s wrong

class Rectangle {
        length: number;
        breadth: number;
        thickness: number;
        area: number;

        constructor(length: number, breadth: number, thickness: number) {
            this.length = length;
            this.breadth = breadth;
            this.thickness = thickness;
            this.area = length * breadth;
        }
    }

    const calculateUsableDimensions = (
        deductions: IDefectWidgetContent['deductions'],
        defaultDimensions: IDefectWidgetContent['defaultDimensions']
    ): Rectangle => {
        const { length: defaultLength, breadth: defaultBreadth, thickness } = defaultDimensions;

        deductions.sort(
            (a, b) => Number(b.length) * Number(b.breadth) - Number(a.length) * Number(a.breadth)
        );

        let lengthSide = 0;
        let breadthSide = 0;

        for (const deduction of deductions) {
            const { corner, length: deductionLength, breadth: deductionBreadth, thickness } = deduction;

            if (corner === 'A' || corner === 'B') {
                lengthSide += Number(deductionLength);
            } else {
                breadthSide += Number(deductionBreadth);
            }
        }

        const remainingLength = Number(defaultLength) - lengthSide;
        const remainingBreadth = Number(defaultBreadth) - breadthSide;

        return new Rectangle(remainingLength, remainingBreadth, 20); // Thickness is set to 20
    };

Here is the playground for this Playground | StoneTEKK Defects Visualizer

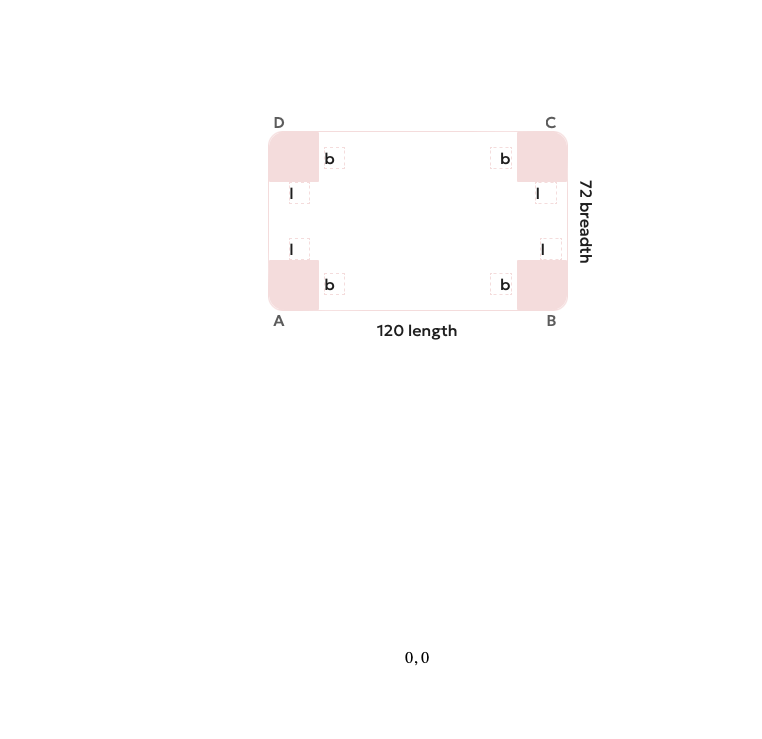
This is what a data of dimensions and deductions looks like

deductions: [
               { corner: 'A', length: 'l', breadth: 'b', thickness: '20' },
               { corner: 'B', length: 'l', breadth: 'b', thickness: '20' },
               { corner: 'C', length: 'l', breadth: 'b', thickness: '20' },
               { corner: 'D', length: 'l', breadth: 'b', thickness: '20' }
            ],
defaultDimensions: { length: '120', breadth: '72', thickness: '20' },

Assume all datatypes in int/Number. Also the visualizer gives accurate representation of the cut-outs. Only it does not calculate the cut-outs correctly and fail to subtract the deductions in a way it can take care of overlaps, and making the available biggest rectangle.

Update

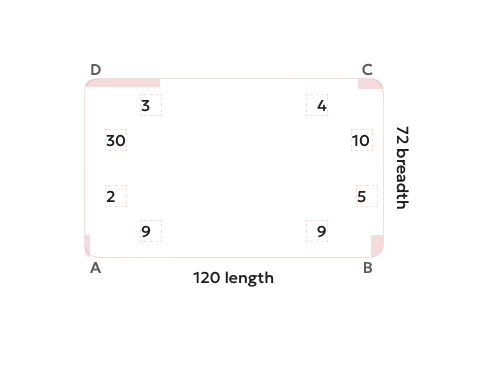
Let’s take a look at this example

Because of these cuts, we will need to make the largest possible rectangle, and it will be smaller rectangle than 120 * 72,

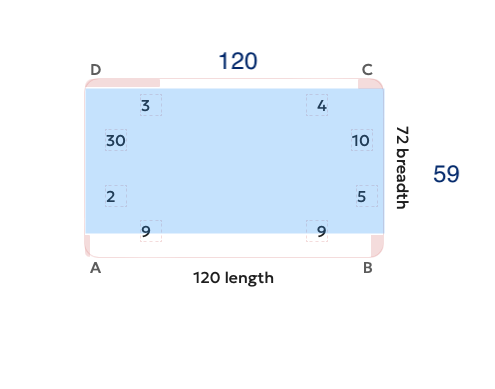
Now if applying brute force, multiple rectangles are possible, I will showcase 2.

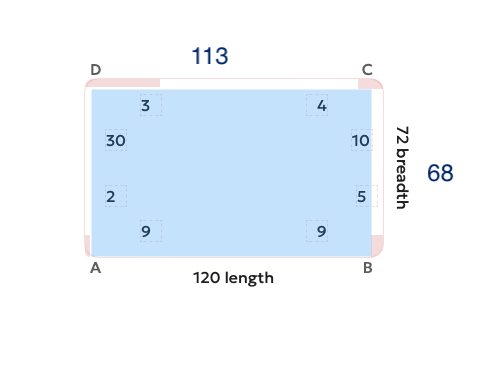
Their areas are 7080 sqft and 7684 sqft. So answer is to return

{ length : 113, breadth: 68, thickness: 20} 

Remember thickness will always remain 20 as we assume for 2D while solving this.