Question 229973 in Javascript Question posted in
A very good W3school tutorial can be found here.

Javascript – Find distance between inside corner of polygon and perimeter of circle

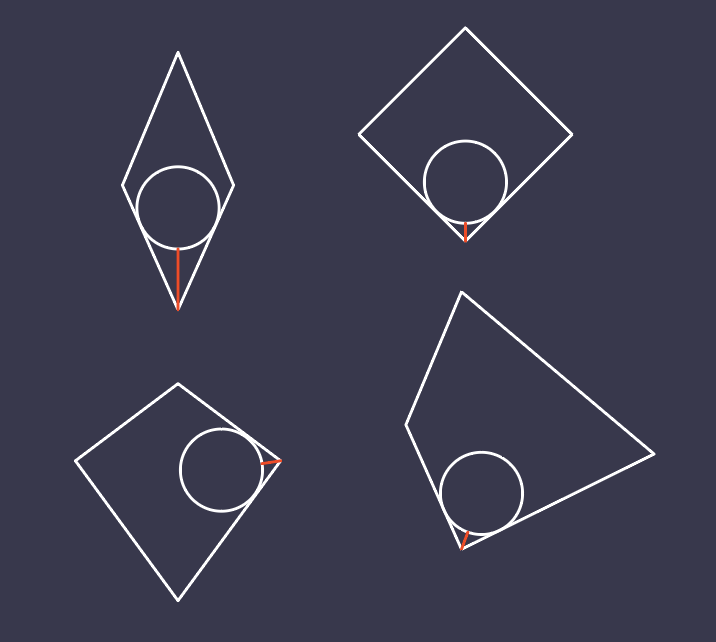
I am trying to calculate the length of the red line in the examples in the image. The information I have is:

  • Coordinates of all points of the polygon
  • Radius of the circle
  • Angle of each corner

I want to place a circle with a given radius as close to a corner of the polygon as possible, meaning the outer tangents between the circle and the corner coordinate is where the circle will rest against the edges – like in the image supplied.

I don’t know how to calculate that little extra space in addition to the circle’s radius in order to keep the circle from intersecting the edges.

enter image description here

Tags:

2

Answers


  1. Chosen as BEST ANSWER
    0

    Image below shows what I did to figure it out. I realized there will always be a right triangle forming between the vertex, the circle's centre, and the point where the circle touches a side of the polygon.

    I know the angle where the circle is approaching, and I know the radius of the circle, so I have both a side length and an angle to work from.

    The distance to the circle centre from the vertex can be figured out using the law of cosines.

    enter image description here


  2. 0

    Okay here’s what you do:

    1. Find the angle formed at the corner that the circle is approaching. You can do this using arctan(arctan2) on the specific line segments in your polygon. Subtract angle 2 from angle 1 and divide by 2 you have the approach angle.

    2. Now do tan(approach angle – smaller angle) which will give you the slope.

    3. The distance along the approach angle will be radius / slope.

    This should work

    Login or Signup to reply.
Please signup or login to give your own answer.

Back To Top
Search