Question 295669 in Javascript Question posted in
A very good W3school tutorial can be found here.

Javascript – Position in x,y of the endpoint of a circle/arc

I am trying to draw lines in a circle like the spokes of a wheel. I am getting stuck because I do not know how to get the coordinates from the end point of the circle. It all works well as long as I draw lines from the rim to the centre of the circle but I am unable to make the lines stop on the inner circle, the hub of the wheel.

<!DOCTYPE html>
<html lang="en" dir="ltr">
  <body>
    <script type="text/javascript">
        const canvas = document.createElement("canvas");
        const ctx = canvas.getContext("2d");
        document.body.appendChild(canvas);
        ctx.beginPath();
        ctx.strokeStyle = "black";
        ctx.arc(75, 75, 70, 0, 2 * Math.PI);
        ctx.arc(75, 75, 20, 0, 2 * Math.PI);
        var part = ( 2 * Math.PI ) / 8;
        for( i=1; i<=8; i++ ) {
            ctx.arc(75, 75, 70, 0, (part*i) );
            ctx.lineTo( 75, 75 );
        }
        ctx.stroke();
    </script>
  </body>
</html>

The result of the above script:
enter image description here

Maybe the solution is simple, but I have only discovered the canvas object in javascript yesterday.
Is there a way to convert the position where the arc ends, to its x and y coordinates?
I know I can calculate these positions using math but I was hoping for an easier solution.

Tags:

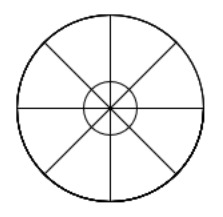
2

Answers


  1. 0

    The solution involves a little bit of trigonometry and math.

    Consider the following code. I replaced the numbers with variables with intuitive names.

    const canvas = document.createElement("canvas");
const ctx = canvas.getContext("2d");
document.body.appendChild(canvas);
ctx.beginPath();
ctx.strokeStyle = "black";

const centerX = 75;
const centerY = 75;
const outerRadius = 70;
const innerRadius = 20;

ctx.arc(centerX, centerY, innerRadius, 0, 2 * Math.PI);
ctx.arc(centerX, centerY, outerRadius, 0, 2 * Math.PI);
var part = (2 * Math.PI) / 8;
for (i = 1; i <= 8; i++) {
  const angle = i * part;
  ctx.moveTo(centerX + innerRadius * Math.cos(angle), centerY + innerRadius * Math.sin(angle));
  ctx.lineTo(centerX + outerRadius * Math.cos(angle), centerY + outerRadius * Math.sin(angle));
}
ctx.stroke();

    Basically, you need to translate the endpoints of the line by a certain amount. This amount will depend on the radius, but changes with the rotation angle. This where sin and cos come in.

    newX = oldX + radius * cos(angle)
newY = oldY + radius * sin(angle)

    radius * sin(a) and radius * cos(a) will give the projection of the rotated distance on the x and y axis

    radius is taken as the radius of inner and outer rims. oldX and oldY are just the centers of these rims.

    This gives the following result.

    result

    Login or Signup to reply.
  2. 0

    If you are looking for a solution without complex maths, you could just draw two circles. Then draw a spoke, rotate() 1/8 turn, add another spoke, and repeat until all the spokes are in.

    const TURN = 2 * Math.PI;

const ctx = document.querySelector("canvas").getContext("2d");
ctx.translate(75, 75); // change the centre point to (75,75)

function circle(radius) {
  ctx.beginPath();
  // arc centre should be (0,0) since we moved the centre to (75,75)
  ctx.arc(0, 0, radius, 0, 1*TURN);
  ctx.closePath();
  ctx.stroke();
}

function spoke(from, to) {
  ctx.beginPath();
  ctx.moveTo(from, 0);
  ctx.lineTo(to, 0);
  ctx.closePath();
  ctx.stroke();
}

ctx.strokeStyle = "black";
circle(20);
circle(70);
for (let i = 0; i < 8; ++i) {
  spoke(20, 70);
  // rotate around the centre
  ctx.rotate((1/8)*TURN); // or 1*TURN / 8
}
    <canvas>wheel</canvas>
    Login or Signup to reply.
Please signup or login to give your own answer.

Back To Top
Search