Jquery - Scaling a rotated rectangle to the minimum size needed to cover it's container

GtwoK
March 26, 2024
98 views
0 votes
2 Answers

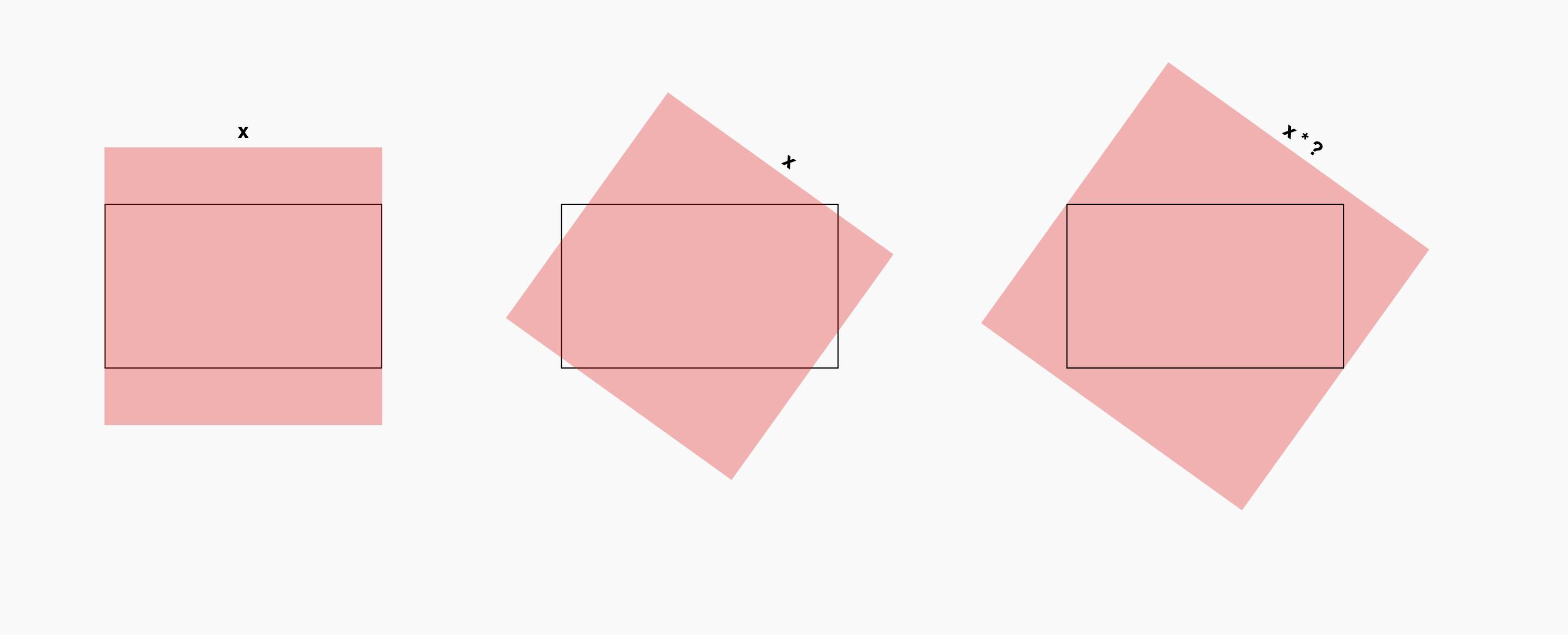
I have a rectangle frame, as well as a second rectangle which can rotate. I would like the determine what minimum scale needs to be applied to the rotating rectangle in order to completely cover the stationary frame.

I have seen solutions to similar problems which solve for the maximum scale to contain the rotating rect within the parent, but I’m not able to decipher how they function in order to figure out what changes would be necessary to modify them for my use case of covering it.

This example shows how to contain the rotating rect, in which the scale to apply is calculated as the current distance from corner to corner over the original distance from corner to corner. Inverting that DOES actually achieve what I’m looking for, but only works if both the child and the parent are the same size. You can see in this codepen how it functions, but if you change the aspect-ratio of #rect1, it no longer works.

This 2nd example works with 2 rectangles of any size (here is a codepen link), however, I can’t decipher how it functions enough to cause the rectangle to cover the frame, rather than be contained to within it.

Would anyone be able to help calculate what is necessary to achieve this?

Answers

If you think about it, the width of the rotating square should be the hypotenuse of the reference square. Then to get the scale, just divide by the width of the rotating square.

Not sure in if you need this in javascript like the examples? You can handle the majority of this with just css. The only thing you need javascript for is to dynamically update the scale css variable, since css doesn’t support this, yet…

let rect = {
      ref: document.querySelector('.rect.ref'),
      rot: document.querySelector('.rect.rot'),
      get_scale: () =>
        Math.hypot(rect.ref.clientHeight, rect.ref.clientWidth) / rect.rot.clientWidth,
      set_scale: () => {
        document.getElementById('scale').innerHTML =
          `:root { --rotate-scale: ${rect.get_scale()}; }`;
      }
  };

//this is just to make it interactive
document.querySelectorAll('input').forEach((input, index, inputs) => {
  input.addEventListener('input', function() {
    rect.ref.style.aspectRatio = ([...inputs].map((i) => i.value).join(' / '));
    rect.set_scale();
  });
});

@keyframes rotate {
  0% { transform: rotate(0deg) scale(var(--rotate-scale)) }
  100% { transform: rotate(360deg) scale(var(--rotate-scale)) }
}

body {
  align-items: center;
  display: flex;
  height: 100vh;
  justify-content: center; }
  
.aspect {
  display: grid;
  left: 0;
  position: fixed;
  top: 0;
  z-index: 1; }

.rect {
  border: 1px solid black;
  box-sizing: border-box;
  position: absolute;
  width: 100px; }

.rect.ref {
  aspect-ratio: 1 / 1; }

.rect.rot {
  animation: rotate 3s linear infinite;
  aspect-ratio: 1 / 1;
  background-color: #ff000050;
  border-color: #ff000050; }

<html>
  <head>
    <style id="scale">
      <!-- start with the hypotenuse of the unit square, aka sqrt(2) -->
      :root { --rotate-scale: 1.412; }
    </style>
  </head>
  <body>
    <div class="aspect">
      <input type="range" min="1" max="10" value="1">
      <input type="range" min="1" max="10" value="1">
    </div>
    
    <div class="rect ref"></div>
    <div class="rect rot"></div>
  </body>
</html>

Using the code base from the codepens you linked to, and using simple trigonometry, the diagonal of the inner rectangle that touches the outer rectangle of minimum size, can be used to determine one of that rectangles’s sides and from that its scale to the original version. Better seen in code than in words:

const cont= document.querySelector('#rect2');
const rot= document.querySelector('#rect1');
const hRot = rot.offsetHeight, h = cont.offsetHeight;
const wRot = rot.offsetWidth, w = cont.offsetWidth;

let t=0; 
const anim= setInterval(rotate, 10);
function rotate(){
    rot.style.transform = "rotate(-" + t + "deg)";
    update(t);
    t += 0.1;
    t = t % 360;
}

function update(T){
  T = T % 180; 
  T = T > 90 ? 180 - T : T;
  const phi = degToRad(T),
     sin_phi = Math.sin(phi),
     cos_phi = Math.cos(phi),
     ratio1 = (w * cos_phi + h * sin_phi) / wRot,
     ratio2 = (w * sin_phi + h * cos_phi) / hRot,
     ratio = Math.max(ratio1, ratio2);
  
  rot.style.transform += " scale(" + ratio + ")";
}

function degToRad(angle){
 return angle * Math.PI / 180;
}

body {
  display: flex;
  justify-content: center;
  align-items: center;
  height: 100vh;
}
#rect1 {
  position: absolute;
  width: 100px;
  aspect-ratio: 2/1;
  background: red;
  opacity: 0.5;
/*   transform: rotate(50deg); */
}
#rect2 {
  position: absolute;
  width: 100px;
  aspect-ratio: 2/1;
  border: 1px solid black;
  opacity: 0.5;
}

<div id="rect1"></div>
<div id="rect2"></div>

The same in the fiddle from the original message; it allows one to play with the sizes and aspect-ratios of the two rectangles.

Please signup or login to give your own answer.

Click here to cancel reply.

Jquery – Scaling a rotated rectangle to the minimum size needed to cover it's container

Answers